Тетраэдр в переводе с греческого означает «четырехгранник». Эта геометрическая фигура обладает четырьмя гранями, четырьмя вершинами и шестью ребрами. Грани представляют собой треугольники. По сути, тетраэдр — это треугольная пирамида. Первые упоминания о многогранниках появились еще задолго до существования Платона.
Сегодня поговорим об элементах и свойствах тетраэдра, а также узнаем формулы нахождения у этих элементов площади, объема и других параметров.
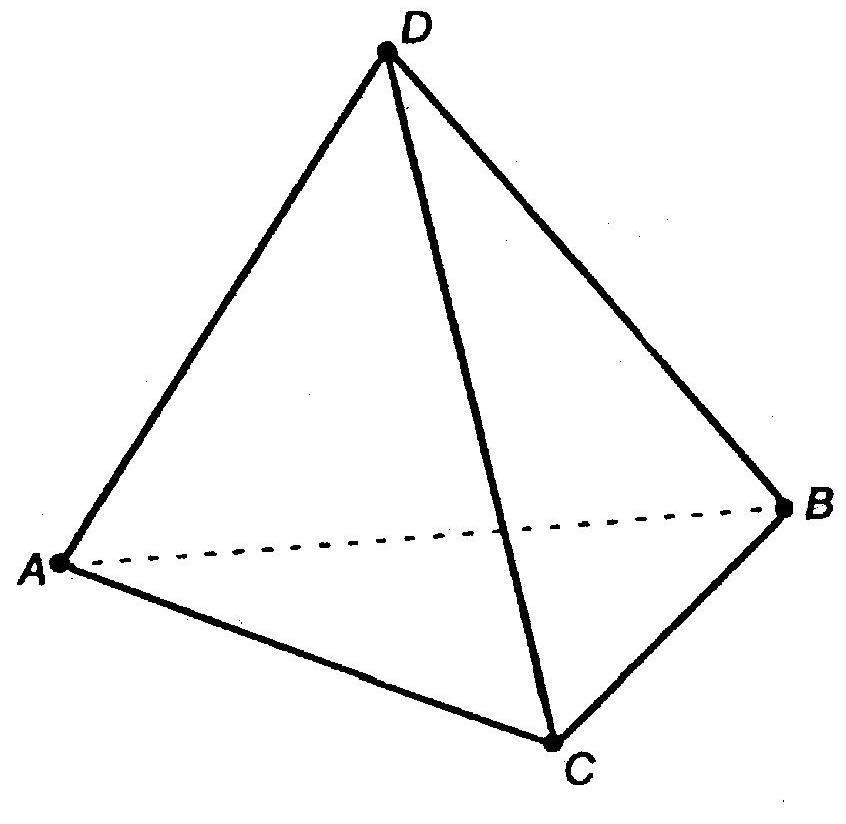
Элементы четырехгранника
Отрезок, выпущенный из любой вершины тетраэдра и опущенный на точку пересечения медиан грани, являющейся противоположной, называется медианой.
Высота многоугольника представляет собой нормальный отрезок, опущенный из вершины напротив.
Бимедианой называется отрезок, соединяющий центры скрещивающихся ребер.
Свойства тетраэдра
1) Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед.
2) Отличительным свойством тетраэдра является то, что медианы и бимедианы фигуры встречаются в одной точке. Важно, что последняя делит медианы в отношении 3:1, а бимедианы — пополам.
3) Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер.
Виды тетраэдра
Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:
- правильным, то есть в основании равносторонний треугольник;
- равногранным, у которого все грани одинаковы по длине;
- ортоцентрическим, когда высоты имеют общую точку пересечения;
- прямоугольным, если плоские углы при вершине нормальные;
- соразмерным, все би высоты равны;
- каркасным, если присутствует сфера, которая касается ребер;
- инцентрическим, то есть отрезки, опущенные из вершины в центр вписанной окружности противоположной грани, имеют общую точку пересечения; эту точку именуют центром тяжести тетраэдра.
Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.
Исходя из названия, можно понять, что так он называется потому, что грани являют собой правильные треугольники. Все ребра этой фигуры конгруэнтны по длине, а грани — по площади. Правильный тетраэдр — это один из пяти аналогичных многогранников.
Формулы четырехгранника
Высота тетраэдра равна произведению корня из 2/3 и длины ребра.
Объем тетраэдра находится так же, как объем пирамиды: корень квадратный из 2 разделить на 12 и умножить на длину ребра в кубе.
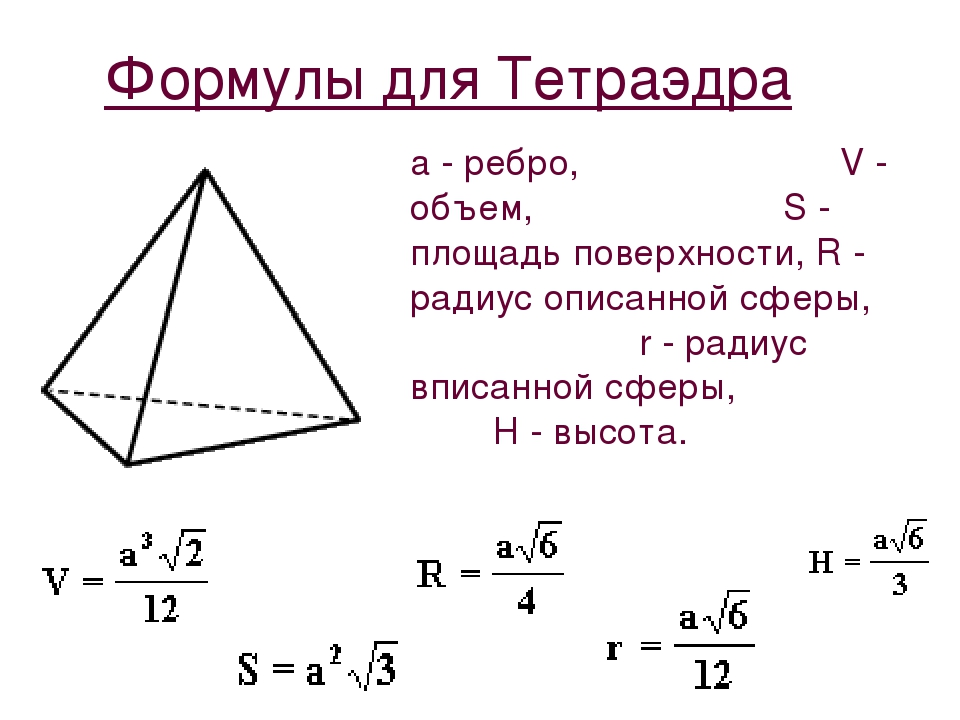
Остальные формулы для расчета площади и радиусов окружностей представлены выше.