Одним из важных оптических приборов, нашедших свое применение при анализе спектров излучения и поглощения, является дифракционная решетка. В данной статье приведена информация, позволяющая понять, что такое дифракционная решетка, в чем заключается принцип ее работы и как самостоятельно можно рассчитать положение максимумов на дифракционной картине, которую она дает.
Дифракция и интерференция
В начале XIX столетия английский ученый Томас Юнг, изучая поведение монохроматического пучка света при его разделении пополам тонкой пластиной, получил дифракционную картину. Она представляла собой последовательность ярких и темных полос на экране. Используя представления о свете, как о волне, Юнг правильно объяснил результаты своих опытов. Картина, которую он наблюдал, возникала благодаря явлениям дифракции и интерференции.
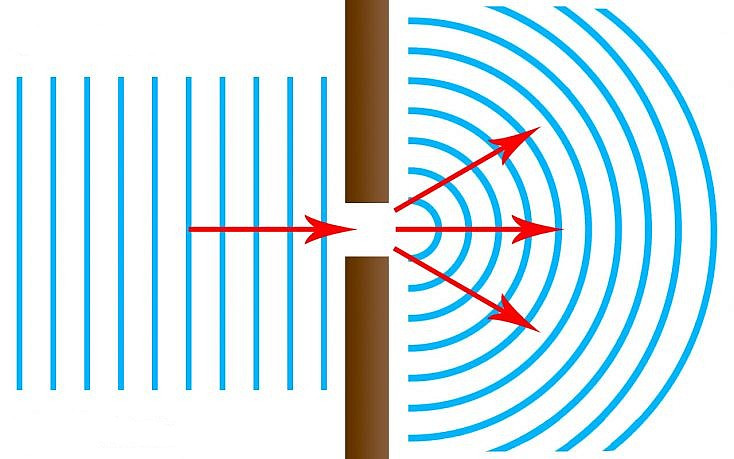
Под дифракцией понимают искривление прямолинейной траектории распространения волны, когда она попадает на непрозрачное препятствие. Дифракция может проявляться в результате огибания волной препятствия (такое возможно, если длина волны намного больше препятствия) либо в результате искривления траектории, когда размеры препятствия сравнимы с длиной волны. Примером для последнего случая является проникновение света в щели и небольшие круглые отверстия.

Явление интерференции заключается в накладывании одних волн на другие. Результатом такого накладывания является искривление синусоидальной формы результирующей волны. Частными случаями интерференции являются либо максимальное усиления амплитуды, когда две волны приходят в рассматриваемую зону пространства в одной фазе, либо полное затухание волнового процесса, когда обе волны встречаются в данной зоне в противофазе.
Описанные явления позволяют понять, что такое дифракционная решетка и как она работает.
Дифракционная решетка

Уже само название говорит, что такое дифракционная решетка. Она представляет собой объект, который состоит из периодически чередующихся прозрачных и непрозрачных полос. Получить ее можно, если постепенно увеличивать число щелей, на которые падает волновой фронт. Это понятие в общем случае применимо для любой волны, однако использование оно нашло только для области видимого электромагнитного излучения, то есть для света.
Дифракционную решетку принято характеризовать тремя главными параметрами:
Период d — это расстояние между двумя щелями, через которые проходит свет. Поскольку длины световых волн лежат в диапазоне нескольких десятых микрометра, то величина d имеет порядок 1 мкм.
Постоянная решетка a — это количество прозрачных щелей, которое находятся на длине 1 мм решетки. Постоянная решетки обратна периоду d. Типичными ее значениями являются 300-600 мм-1. Как правило, значение a написано на дифракционной решетке.
Общее количество щелей N. Эту величину легко получить, если умножить длину дифракционной решетки на ее постоянную. Так как типичные длины составляют несколько сантиметров, то каждая решетка содержит около 10-20 тысяч щелей.
Прозрачные и отражающие решетки
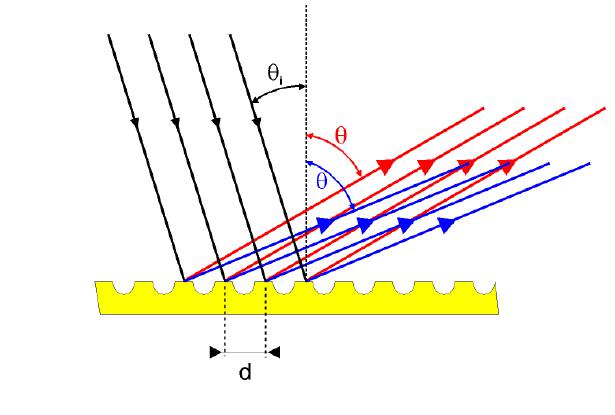
Выше было описано, что такое дифракционная решетка. Теперь ответим на вопрос о том, что в действительности она собой представляет. Существуют два вида таких оптических объектов: прозрачные и отражающие.
Прозрачная решетка — это стеклянная тонкая пластинка или пластинка из прозрачного пластика, на которую нанесены штрихи. Штрихи дифракционной решетки являются препятствием для света, через них он не может пройти. Ширина штриха — это и есть вышеупомянутый период d. Оставшиеся между штрихами прозрачные зазоры играют роль щелей. При выполнении лабораторных работ используют этот вид решеток.
Отражающая решетка — это металлическая или пластиковая отполированная пластинка, на которую вместо штрихов нанесены бороздки определенной глубины. Период d — это расстояние между бороздками. Отражающие решетки часто используют при анализе спектров излучения, поскольку их дизайн позволяет распределять интенсивность максимумов дифракционной картины в пользу максимумов более высокого порядка. Оптический диск CD — яркий пример этого вида дифракционной решетки.
Принцип работы решетки
Для примера рассмотрим прозрачный оптический прибор. Предположим, что на дифракционную решетку падает свет, имеющий плоский фронт. Это очень важный момент, поскольку приведенные ниже формулы учитывают, что волновой фронт является плоским и параллельным самой пластинке (дифракция Фраунгофера). Распределенные по периодическому закону штрихи вносят в этот фронт возмущение, в результате которого на выходе из пластинки создается ситуация, будто работают множество вторичных когерентных источников излучения (принцип Гюйгенса-Френеля). Эти источники приводят к появлению дифракции.
От каждого источника (щели между штрихами) распространяется волна, которая является когерентной всем остальным N-1 волнам. Теперь предположим, что на некотором расстоянии от пластинки помещается экран (расстояние должно быть достаточным, чтобы число Френеля было намного меньше единицы). Если смотреть на экран вдоль перпендикуляра, проведенного к центру пластинки, то в результате интерференционного наложения волн от этих N источников для некоторых углов θ будут наблюдаться яркие полосы, между которыми будет тень.
Поскольку условие интерференционных максимумов является функцией длины волны, то если падающий на пластинку свет был белым, на экране будут появляться разноцветные яркие полосы.
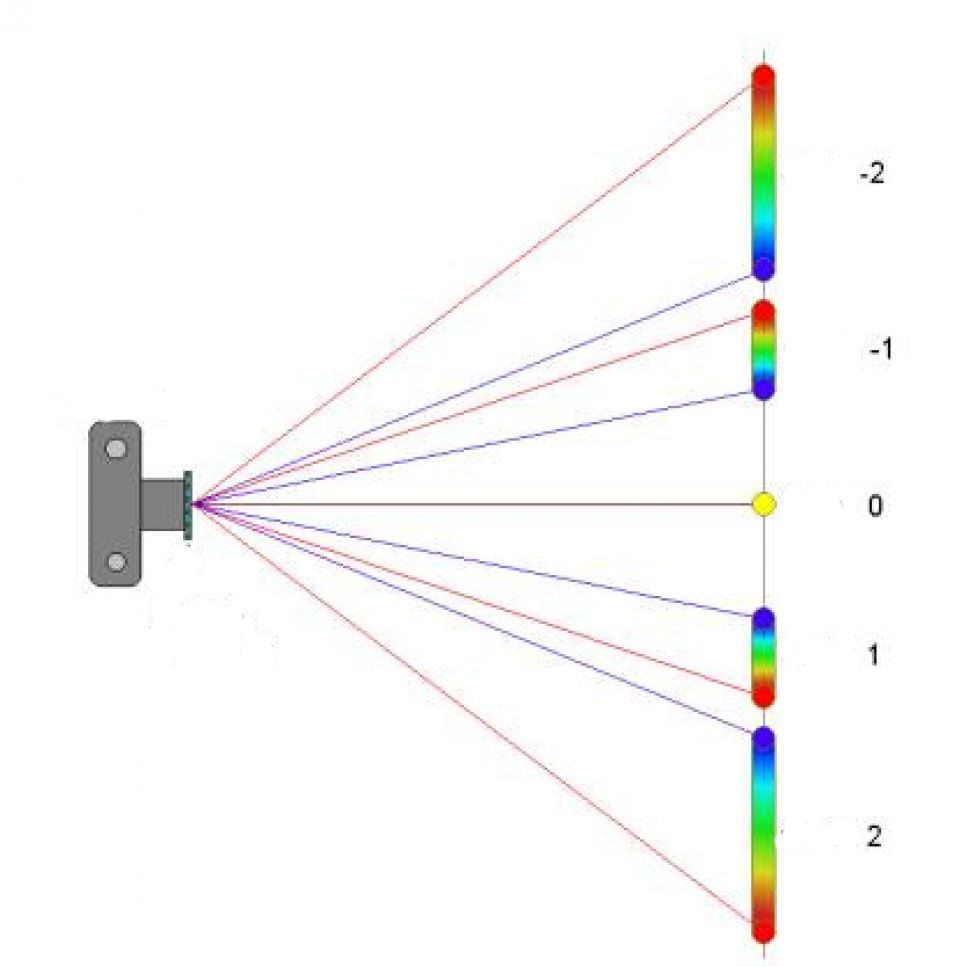
Основная формула
Как было сказано, падающий плоский фронт волны на дифракционную решетку отображается на экране в виде ярких полос, разделенных областью тени. Каждая яркая полоса называется максимумом. Если рассмотреть условие усиления волн, приходящих в рассматриваемую область в одинаковой фазе, то можно получить формулу максимумов дифракционной решетки. Она имеет следующий вид:
sin(θm) = m*λ/d
Где θm — это углы между перпендикуляром к центру пластинки и направлением на соответствующую линию максимума на экране. Величина m называется порядком дифракционной решетки. Она принимает целые значения и ноль, то есть m = 0, ±1, 2, 3 и так далее.
Зная период решетки d и длину волны λ, которая падает на нее, можно рассчитать положение всех максимумов. Отметим, что вычисленные по формуле выше максимумы называются главными. В действительности между ними существует целый набор более слабых максимумов, которые часто в эксперименте не наблюдаются.
Не стоит думать, что от ширины каждой щели на дифракционной пластинке картина на экране не зависит. Ширина щели не влияет на положение максимумов, однако она влияет на их интенсивность и ширину. Так, с уменьшением щели (с увеличением числа штрихов на пластинке) снижается интенсивность каждого максимума, а его ширина увеличивается.
Дифракционная решетка в спектроскопии
Разобравшись с вопросами о том, что такое дифракционная решетка и как находить максимумы, которые она дает на экране, любопытно проанализировать, что будет происходить с белым светом, если им облучить пластинку.
Выпишем снова формулу для главных максимумов:
sin(θm) = m*λ/d
Если рассматривать конкретный порядок дифракции (например, m = 1), то видно, что чем больше λ, тем дальше от центрального максимума (m = 0) будет находиться соответствующая яркая линия. Это означает, что белый свет расщепляется на ряд цветов радуги, которые отображаются на экране. Причем, начиная от центра, сначала будут появляться фиолетовый и синий цвета, а затем будут идти желтый, зеленый и самый дальний максимум первого порядка будет соответствовать красному цвету.
Свойство дифракционной решетки длины волн используется в спектроскопии. Когда необходимо узнать химический состав светящегося объекта, например, далекой звезды, то ее свет собирают зеркалами и направляют на пластинку. Измеряя углы θm, можно определить все длины волн спектра, а значит, и химические элементы, которые их излучают.
Ниже приводится видео, которое демонстрирует способность решеток с разным числом N расщеплять свет от лампы.
Понятие «угловая дисперсия»
Под этой величиной понимают изменения угла возникновения максимума на экране. Если изменить на небольшую величину длину монохроматического света, то получим:
D = dθm/dλ
Если левую и правую части равенства в формуле для главных максимумов продифференцировать по θm и λ соответственно, то можно получить выражение для дисперсии. Оно будет равно:
D = m/(d*cos(θm))
Дисперсию необходимо знать при определении разрешающей способности пластинки.
Что такое разрешающая способность?
Говоря простыми словами, это способность дифракционной решетки разделять две волны с близкими значениями λ на два отдельных максимума на экране. Согласно критерию лорда Рэлея, две линии можно различить, если угловая дистанция между ними окажется больше половины их угловой ширины. Полуширина линии определяется по формуле:
Δθ1/2 = λ/(N*d*cos(θm))
Различие между линиями в соответствии с критерием Рэлея возможно, если:
Δθm > Δθ1/2
Подставляя формулу для дисперсии и полуширины, получаем конечное условие:
Δλ > λ/(N*m)
Разрешающая способность решетки повышается с увеличением числа щелей (штрихов) на ней и с ростом порядка дифракции.
Решение задачи
Применим полученные знания для решения простой задачи. Пусть на дифракционную решетку падает свет. Известно, что длина волны равна 450 нм, а период решетки составляет 3 мкм. Какой максимальный порядок дифракции можно наблюдать на кране?
Для ответа на вопрос следует подставить данные в уравнение решетки. Получаем:
sin(θm) = m*λ/d = 0,15*m
Так как синус больше единицы быть не может, тогда получаем, что максимальный порядок дифракции для указанных условий задачи равен 6.